Ulams Triangel
Ordnet man Primzahlen gemäss Ulam in einer Spirale an, erkennt man ein Muster, Strukturen in den Zahlen. Ich denke noch schöner erkennt man diese, wenn die Zahlen in einem Dreieck, einem Triangel anordnet werden. Man beginnt oben links und geht dann ein Feld nach unten, Zahl um Zahl diagonal nach oben bis zum Rand, springt wieder nach unten zur nächsten Diagonalen. Primzahlen werden dabei markiert, andere Zahlen nicht:
Die Schönheit dieser Anordnung erkennt man gut, wenn man einen Triangel mit der Seitenlänge 1000 aufspannt, hier gibt es auf vielen Diagonalen Häufungen von Primzahlen, auch horizontale Linien und viele andere feine Strukturen:
Man könnte nun meinen diese Häufungen entsprechen zumindest zum Teil der bekannten Formel von Euler, z. B. n^2 – n + 41. Das nachfolgende Bild zeigt aber, dass diese einer anderen Logik folgen, in den beiden Triangeln wurden sie dazu markiert: rot alle Formelwerte die Primzahlen sind – und gelb alle, die keine sind:
Die obige Formel gilt als sehr guter Indikator, um eine Primzahl zu finden: rund 50% aller daraus generierten Kandidaten sind Primzahlen. Wie hoch ist dieser Wert bei den Zahlen, die auf den Diagonalen, den auffälligen Linien des Triangels liegen? Durch etwas Rechnerei sind die Formeln leicht bestimmt: Dialogen, die am oberen Rand starten, lässt sich mit 2(n + i / 2)^2 – 4n – 1.5i + 2 beschreiben. Diagonalen die am linken Rand starten mit 2(n + i / 2)^2 – 4n – 2.5i + 3. Dabei ist i der Startpunkt, also die i-te Zelle von oben links gesehen, und n ein fortlaufende Zähler. Hier zwei Beispiele für i = 4-L und 25-O, L und O stehen jeweils für Links (beginnend) und Oben (beginnend):
Mit diesen beiden allgemeinen Formeln, lässt sich nun für i von 1 bis 500 prüfen, wie viele der generierten Zahlen (bis 4 Mio.) Primzahlen sind: Die besten Werte findet sich für i=58-O und 400-L mit jeweils 48% und 54% Treffer:
Die beste Formel lauten somit: 2n^2 + 796n + 79003
Die oben aufgeführte Eulersche Formel hat bei diesen relativ kleinen Zahlen (bis 4 Mio.) eine Trefferquote von „nur“ 51%. Prüft man aber bei beiden Formel die ersten 1000 Elemente liegt Euler mit 58% vor 400-L mit 54%. Aber immerhin, vier Prozentpunkte schlechter als Euler, ist doch Ok, oder?
Nachtrag
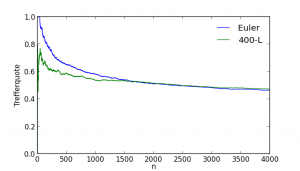
Wenn man bis 36 Mio. rechnet, nimmt die Quote von 400-L zwar auf 47.2% ab, allerdings – nach meinen Berechnungen – auch die Quote der Euler-Formel, auf 44.0%. Kann das sein?! Nimmt man als Kriterium die ersten 4000 Zahlen der Formel, hat 400-L wieder 47.2% und Euler 46.5%. Bei diesem zweiten Test schneidet Euler etwas besser ab, da dessen Zahlen kleiner und so tendentiell eher prim sind. Aber auch hier wird er geschlagen. Der nachfolgende Graph zeigt die Trefferquote im Bezug auf die ersten n Formelwerte:
Kurze Tests mit n=30’000 bestätigen diese Ergbniss. Auch dass 400-L (gemäss diesem Kriterium) besser ist als andere bekannte Generatoren wie n^2 – 79n + 1601 oder 36n^2 – 810n + 2753. Gut gemacht 400-L!
Mit diesem Programm wurden alle obigen Ergebnisse gemessen: test_primzahl.zip
Christian Rusche, 2012