Abstand halten
Man kann einfach zeigen, dass der Abstand zwischen Primzahlen beliebig gross wird. Aber wie weit liegen sie üblicherweise auseinander? Und wie verteilen sich die Abstände? Normalverteilt? Oder zufällig? Wir werde gleich sehen, dass die Zahl 6 dabei eine Rolle spielt.
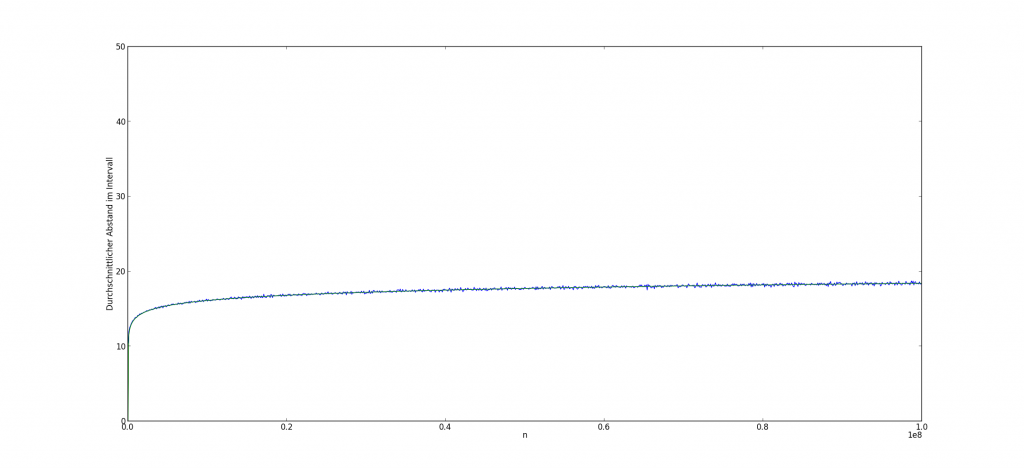
Zuerst wollen wir uns ansehen, wie sich die Abstände bei grösser werdenden Zahlen entwickeln. Dafür teilen wir alle Zahlen zwischen 1 und 108 in 1000 Intervalle auf, und messen für jedes dieser Intervalle den durchschnittlichen Abstand zwischen den Primzahlen:
Der gemessene, blaue Wert liegt so nahe beim theoretisch vorhergesagten, dem grün eingezeichnete Logarithmus von n, das es Freude macht! PS: Ich konnte zwar auf die Schnelle den zugehörigen mathematischen Satz nicht finden – aber es wird ihn sicher geben.
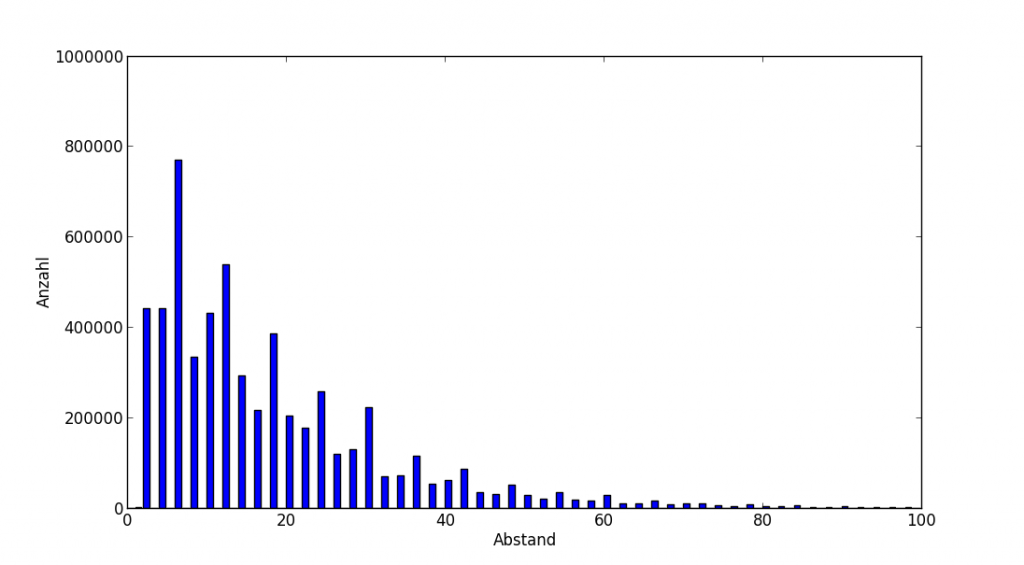
Nun wollen wir sehen, wie sich dieser Durchschnitt zusammensetzt, welche Abstände wie häufig vorkommen (wieder für alle bis 108):
Der Abstand 1 ist sehr selten, er kommt genau einmal vor, zwischen 2 und 3. Es ist auch der einzige ungerade Abstand, natürlich. Die Abstände 2 und 4 kommen, bei dieser Grössenordnung etwas gleich oft vor. Alle Abstände, die ein Vielfaches von 6 sind, übertreffen ihre 4 Abstandsnachbarn immer & deutlich, sie scheinen speziell.
Die Struktur dieser Verteilung ist nicht ganz unwichtig: Würde man etwa feststellen, dass sich die Verteilung einer statistischen Regel unterwirft wie es z. B. die Anzahl Primfaktoren tun, dann wäre die Vermutung zu den Primzahlzwillingen bewiesen, weil dann zwingend Primzahlen mit dem Abstand 2 vorkommen, ja hinzukommen müssen, je grösser man n wählt.
Nachtrag folgt bestimmt!
PS: Hier alle für diesen Artikel verwendeten Computerprogramme: abstand.zip
Christian Rusche, 2012