Gewinner und Verlierer?
Zahlen lassen sich auf viele Arten klassifizieren, z. B. gemäss der Anzahl Teiler, oder aus welchen Primfaktoren sie zusammengesetzt sind. Eine interessante, wenn wohl auch wenig praxisnahe Klassierung ist die Anzahl verschiedener Primfaktoren einer untersuchten Zahl.
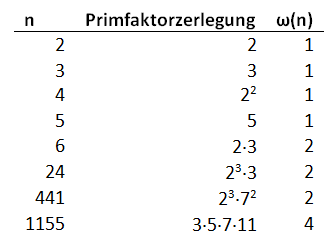
Nennen wir die Funktion, die diese Anzahl bestimmt ω. Für jede Primzahl ist ω = 1, den sie lässt sich nur durch sich selber und 1 teilen, aber die 1 ist trivial und wollen wir nicht mitzählen. ω von 6 ist 2, denn man kann die Zahl in 2 und 3 zerlegen, und auch ω von 12 ist 2, auch hier sind nur 2 und 3 Primfaktoren. Für 32 gilt wieder ω = 1, denn der einzige Primfaktor ist 2. Noch einige Beispiele:
So lässt sich jeder ganze Zahl n einer Zahl ω zuordnen. ω ist nicht begrenzt, man kann aus jeder Zahl n mit ω(n) = ωn leicht einen Zahl mit ωn+1 konstruieren, z. B. indem man n mit einer Primzahl multipliziert, die grösser ist als die Wurzel von n. Grössere ω zeigen sich nicht so schnell, so muss man bis 108 nur mit ω ≤ 8 rechnen. Leider: Die Funktion ω ist recht garstig, sie scheint kaum innere Schönheit zu haben, so sagt ω(n+m) und ω(n·m) wenig über ω(n) und ω(m) aus oder umgekehrt.
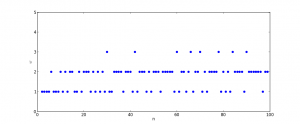
Mit kleinen und wenigen Zahlen macht ω auch optisch nicht viel her. Hier z. B. alle ω für die Zahlen 2 bis 100:
Etwas attraktiver, wenn auch noch nicht wirklich erhellend, wird das Bild, wenn man berechnet, wie viele Zahlen kleiner oder gleich n einen bestimmten Wert ω haben, Hier die zugehörige Stufenfunktion für n ≤ 1000 und n ≤ 10000:
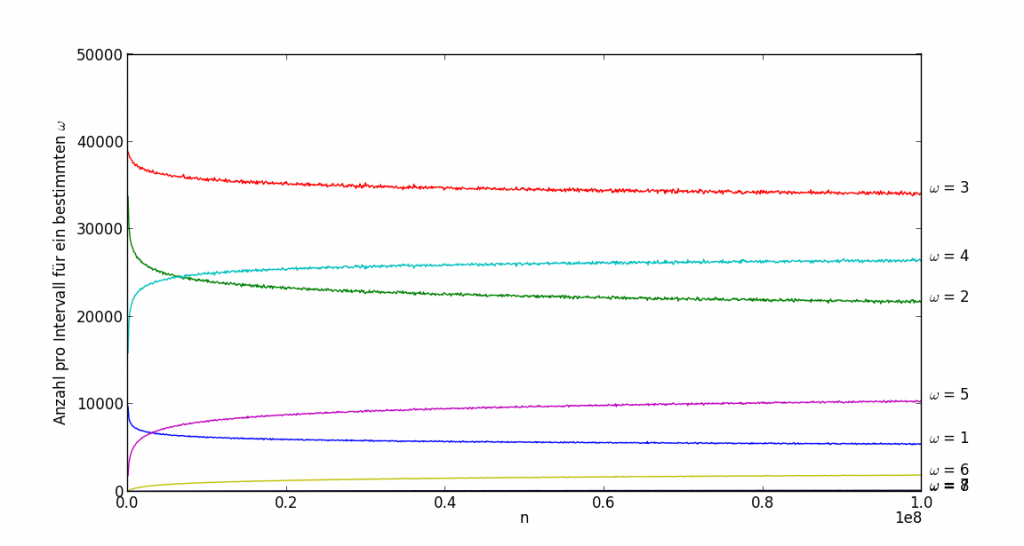
Sieht der linke Graph etwas interessant aus, überholt doch ω = 3 die Primzahlen und deren Potenzen, wirkt der rechte Graph doch sehr bieder, kaum Spass versprechend. Aber: Richtig interessant wird ω erst, wenn man es mit grossen Zahlen konfrontiert, gleichzeitig wechseln wir noch ein weiteres Mal die Darstellungsform: Im Folgenden werden die Zahlen mit einem bestimmten ω nicht aufsummiert, sondern pro Intervall gezählt, wir bestimmen sozusagen die Dichte. Der folgende Graph unterteilt beispielsweise die Zahlen bis 108 in 1000 Intervalle und zählt die Zahlen pro Intervall mit einem bestimmten ω. Das Schöne an dieser Darstellung: die Summe aller Elemente ergibt die Gesamtzahl aller Zahlen im Intervall: Ein Verdrängungskampf!
Es scheint zwei Arten von ω zu geben: Gewinner und Verlierer. Primzahlen (zusammen mit ihren Potenzen) und ω = 2 und 3 sind Verlierer – arme Primzahlen! Aber 4 und 5 nicht. Oder liegt das an den Grössenverhältnissen? Wird auch 4 und 5 bald von 6 und 7 abgelöst? So scheint es auf den ersten Blick nicht; bereits in ihrer Jugend, bei kleinen n, unterscheiden sich die Gewinner und Verlieren. Wie im richtigen Leben?
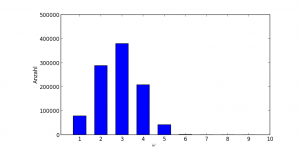
Aber wie so oft in der Mathematik darf man sich nicht auf den ersten Eindruck verlassen. Die Verteilung von ω wurde bereits 1940 von Erdös und Kac behandelt. Sie konnten zeigen, dass ω annähernd normalverteilt ist, und damit bei sehr grossen n auch grössere ω im Mittelpunkt stehen werden. Für alle n ≤ 108 sieht man diese Verteilung hier schön:
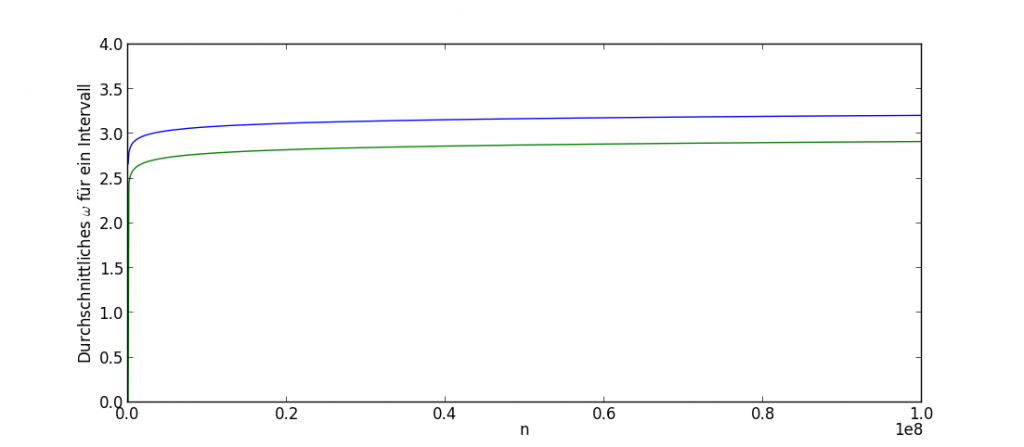
Eine andere theoretische Erkenntnis, dieses Mal von G. H. Hardy und S. Ramanujan, besagt, dass sich der Durchschnittswert für ω nur sehr, sehr langsam, und zwar im wesenlichen wie der doppelt angewendete, natürliche Logarithmus entwickickelt. Auch diesen Zusammenhang können wir schön nachvollziehen (die grüne Linie ist der doppelte Logarithmus, die blaue der „gemessene“ Durchschnitt von ω):
Es ist wie so oft im Mathematikerleben: Aus der Vergangenheit lässt sich nicht viel über die Zukunft aussagen, schon gar nicht wer ein Gewinner ist und wer ein Verlierer.
Verallgemeinerte Goldbachsche Vermutung
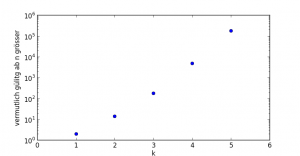
Jede ganze, gerade Zahl grösser 2 kann als Summe zweier Primzahl geschrieben werden? Tönt realistisch und hält auch jedem Versuch stand. Und lässt sich doch so schwer beweisen? Vielleicht geht es einfacher, wenn man den Satz etwas aufweicht? Man könnte ihn verallgemeinern, behaupten jede Zahl lässt sich als Summer zweier Zahlen n1 und n2 schreibe, mit ω(n1) = ω(n2) = k. Für k = 1 wäre es (in etwa) die Golbachsche Vermutung. k = 2 geht auch, zeigt zumindest ein Experiment bis zu unseren üblichen 108, allerdings erst für n grösser 14. Ähnlich auch für k = 3, da aber erst für n grösser 178, aber dann immerhin für jedes n bis 108. Und so geht es weiter: für k = 4 ist die Grenze bei 4766 und für k = 5 gilt der Satz – vermutlich – für alle n grösser 178918. Trägt man diese Zahlen mit einer logarithmischen Achse auf, sieht man einen Zusammenhang:
Kür k = 6 scheint die Grenze bei etwa 107 zu liegen? Vielleicht lohnt es sich, das genauer zu untersuchen?
Nachtrag: k = 6 gilt tatsächlich für n > 9143782.
PS: Alle für diesen Artikel verwendeten Computerprogramme finden sich hier: teiler.zip
Christian Rusche, 2012